確率分布関数と確率密度関数

名前が似ていてややこしいので、簡単に説明する。

厳密には数学的定義があると思うが、簡単にイメージするための定義を説明すると、確率分布関数は－∞で０、＋∞で１の値をとる単調増加関数であって、それを微分したものが確率密度関数である。不連続な関数も取り扱っているので実際に計算するときには、グラフを書いたほうがわかりやすいかもしれない。

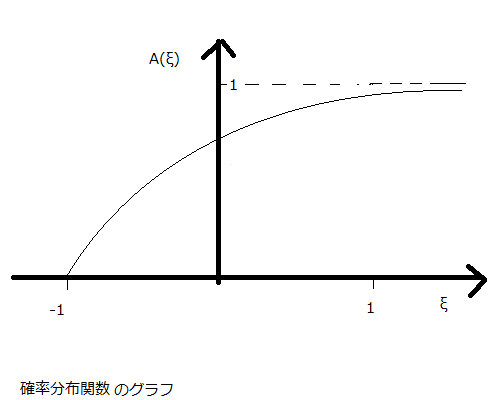
活発度aの予想誤差に関する確率分布関数をAと置いている。今活発度は正の実数を前提としているので、予想誤差の式\( a/ \hat E(a) -1 \)から、今予想誤差の最小値は－１であることがわかる。したがってA（X)のグラフは、－∞から-1の区間は０であって、そこから1の値まで増加する関数となる。

テキストの数学付録(a)にでてくるA（ξ）の例題として一様分布の場合と指数分布の例がでてくる。あとでこれらのA(ξ）についての最適価格を計算する。一様分布の場合のグラフを下記に示す。

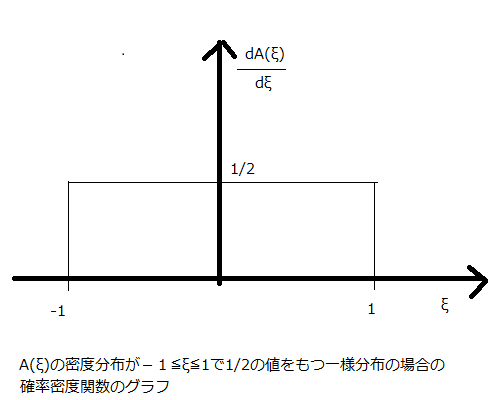
確率密度関数(一様分布)のグラフ

確率分布関数（一様分布）のグラフ

確率密度関数がξ≧－1の範囲で\( e^{-(1-ξ)} \)の確率分布関数のグラフを下記に示す。なお図は省略しているが、この場合の確率密度関数は、A(ξ)=1/2で上下折り返したようなグラフになっている。

確率分布関数（指数関数）のグラフの例